概要

[1612.08083] Language Modeling with Gated Convolutional Networks

自然言語処理の分野ではRNNが一般的だが、LSTMのようなゲート機構付きのCNNを提案
CNNはRNNと比べて並列化が容易であり、高速化ができる
RNNに比べ僅かに精度は劣るが、大幅な高速化を達成した
ゲート機構の付いた活性化関数（Gated Linear Unit, GLU)が収束に必要なエポック数の削減に貢献していることを確認

手法

ゲート機構

いわゆるゲート機構とは

$f \left(\bf{x}, \bf{y} \right) = \bf{x} \otimes \sigma \left( \bf{y} \right)$

で表現されるモデルのことで、$ \sigma \left( \bf{y} \right) $の出力により$ \bf{x} $を出力するか判断できる仕組みのことである。

Gated Convolutional Neural Network (GCNN)

ネットワーク全体は以下の通り（元論文より引用）

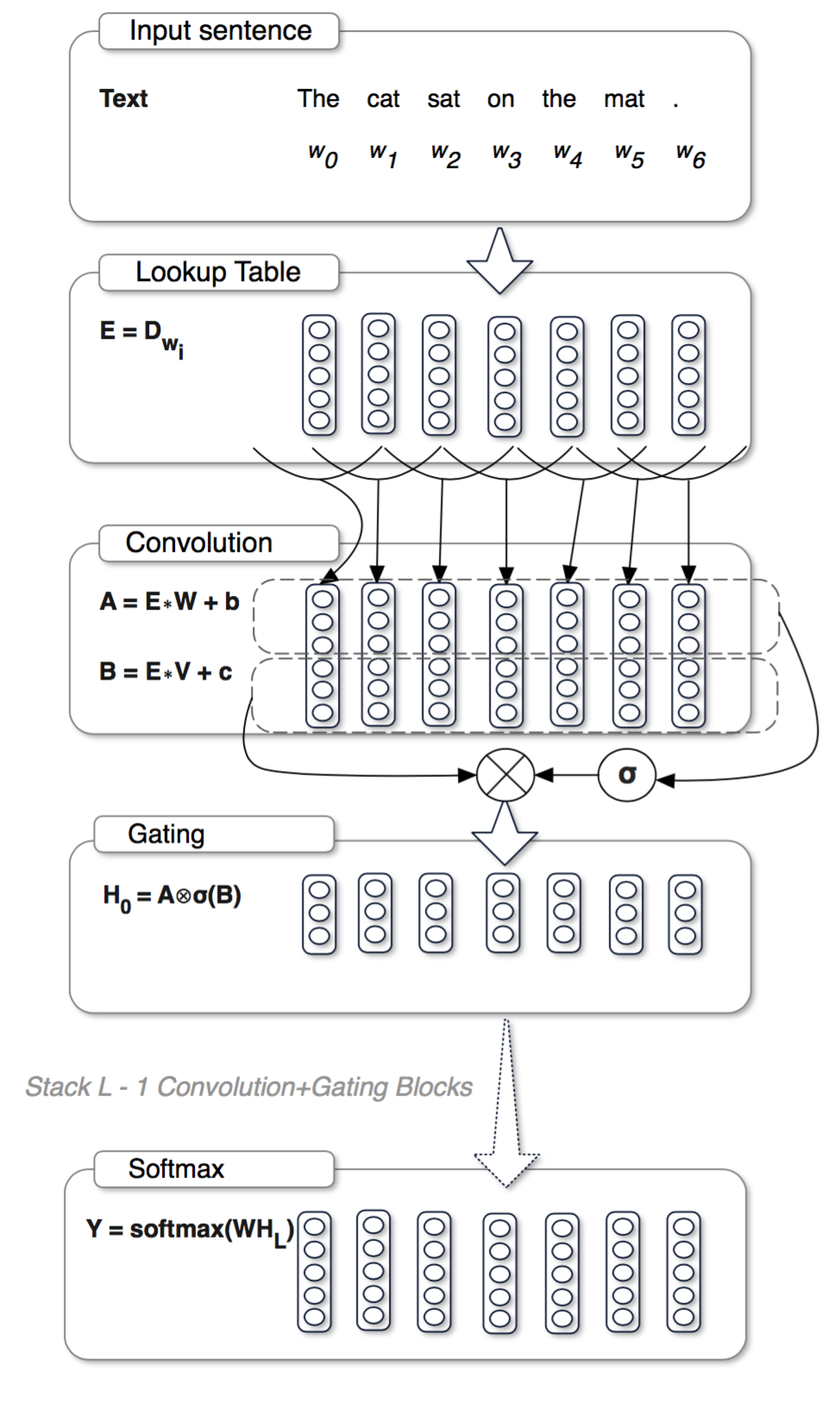
network

TokenizeされたTextをEmbedした上でConvolution層に投げる。Convolution層では2種類の出力A, Bを計算し、Aは実際の出力、Bはゲートの開閉判断に用いられる。

ゲート機構の必要性・存在意義

RNNは、時系列長だけスタックしたネットワークであり、時系列長が長くなるに連れ、Gradient Vanishmentの問題が顕著になる。 LSTMでは、入出力にシグモイドによるゲート機構を設けることでこの問題に対処する。

一方今回のモデルではモデルの深さは時系列長ではなくConcolutionのスタック数に依存するためRNNほどGradient Vanishmentは顕著ではない。今回、GLUはGradient Vanishment対策ではなく、Attentionの目的で導入されている。CNNにゲート機構を導入する有効性については[1606.05328] Conditional Image Generation with PixelCNN Decodersで言及されている。

Gated Linear Unit (GLU)

LSTMのゲート機構は次のように表現できる（Gated Tanh Unit, GTU)

$f \left( \bf{x} \right) \otimes \sigma \left( \bf{y} \right)$

活性化関数$ f \left( \cdot \right) $は通常tanhを用いる。この微分は

$\begin{align} \nabla \left[ f \left( \bf{x} \right) \otimes \sigma \left( \bf{y} \right) \right] &= \nabla f \left( \bf{x} \right) \otimes \sigma \left( \bf{y} \right) + f \left( \bf{x} \right) \otimes \nabla \sigma \left( \bf{y} \right) \\ &= f' \left( \bf{x} \right) \nabla \bf{x} \otimes \sigma \left( \bf{y} \right) + f \left( \bf{x} \right) \otimes \nabla \sigma \left( \bf{y} \right) \end{align}$

となる。右辺第一項より、$ \sigma \left( \bf{y} \right) = 1 $でゲートが開いていても、誤差勾配$ \nabla \bf{x} $は$ f’ \left( \bf{x} \right) $だけ減少してしまう。このため、LSTMを多層にStackすると誤差勾配が指数関数的に消失してしまう。

GLUの場合は

$\nabla \left[ \bf{x} \otimes \sigma \left( \bf{y} \right) \right] = \nabla \bf{x} \otimes \sigma \left( \bf{y} \right) + \bf{x} \otimes \nabla \sigma\left( \bf{y} \right)$

右辺第一項により、勾配は消失することなく前層へ伝搬することが出来る。

評価

評価方法

データセットとして、Google One Billion Word Benchmark とWikiText-103を使用。文が途中まで与えられ、次に登場する単語を予測し、そのPerplexityで評価。学習にはGradient ClippingとWeight Normalizationを使用。

Perplexity

例えば、A, B, Cの3つのラベルから1つ正解を選ぶタスクがあるとする。

あるモデルMで予測された確率が (A=0.6, B=0.3, C=0.1) で、正解ラベルがCだったら、これは 「候補数10個の問題からランダムチョイスで正解を選択する問題」 と難易度が等しいと考えられる。なので、Perplexity=10となる。

正解ラベルを高い確率で予測することが重要であり、その他のラベルの確率分布は関係ない、という評価指標。

結果

精度

Google One Billion Word Benchmarkの場合のPerplexity、比較対象はGoogle One Billion Word Benchmarkの元論文のモデル。

Model	Perplexity (PPL)	Training Time [week]	# of GPU
LSTM-1024	48.7	3	32
GCNN-8 (proposed)	44.9	2	1

精度が若干下がっているが、学習に要した時間・使用プロセッサ数が大幅に減っている。

活性化関数

EpochとPPLの関係、左がWikiText-103、右がGoogle One Billion Word

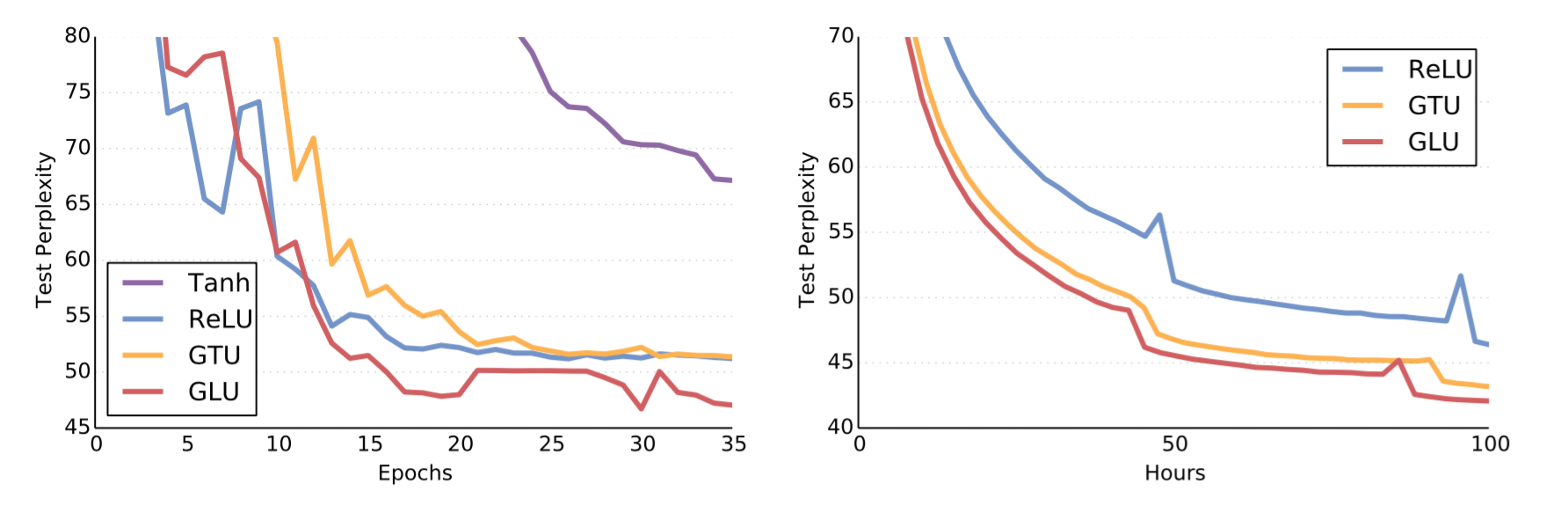
（元論文より引用） Learning Curve

ゲート機構を用いたものが精度・収束速度共に良いことがわかる。

ゲート機構の亜種

GLUとLinear form( $ \bf{h} = \bf{X} * \bf{W} + \bf{b} $ )、Bilinear form( $ \bf{h} = \left( \bf{X} * \bf{W} + \bf{b} \right) \otimes \left( \bf{X} * \bf{V} + \bf{c} \right) $ )を比較。Bilinear formはシグモイドがかかっていないことに注意。

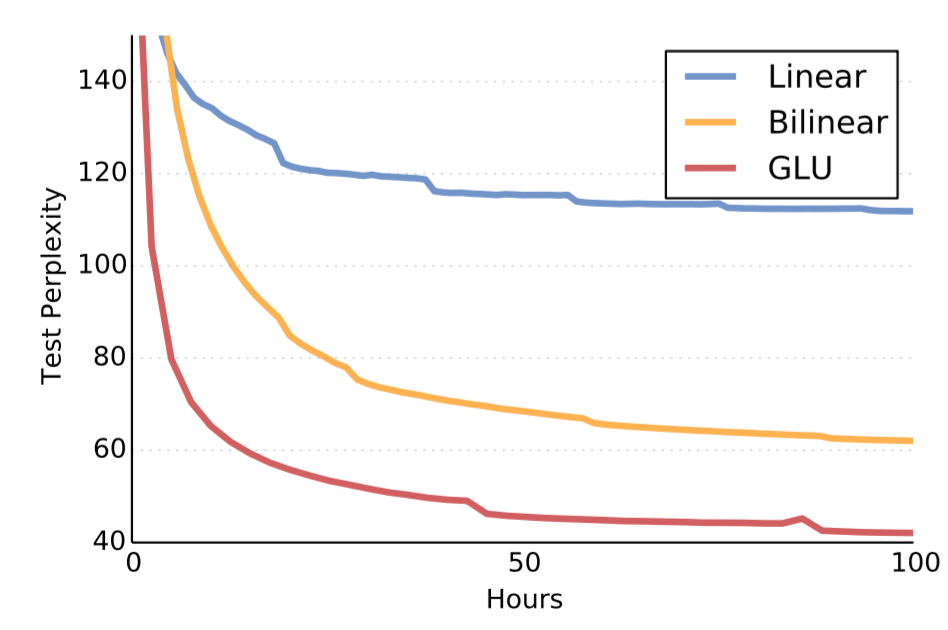
（元論文より引用） Learning Curve

GLUが学習速度・精度ともに良い。

学習方法と精度・速度

Gradient Clipping, Weight Normalizationを使用しなかった場合と比較。

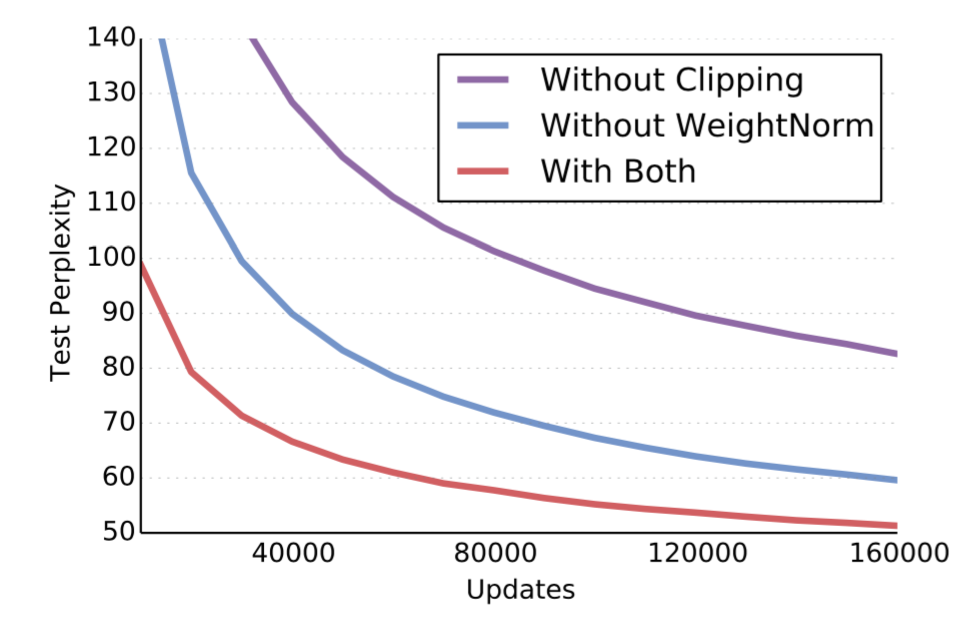
（元論文より引用） Learning Curve

WeightNormを使うと、学習係数の初期値を0.01から1にしても学習ができ、結果的に収束までの時間が早くなった。 Gradient ClippingもWeight Normalizationも処理に要するオーバーヘッドはわずかで、無視できる。