概要

[1703.09746] Coordinating Filters for Faster Deep Neural Networks

• DNNのLow-Rank Approximatios(LRA)に関する研究
• LRAしやすいようにパラメータを学習する方法を提案
• AlexNetを精度を落とさずに2倍高速化するなど、様々なモデルで速度向上

手法：Force Regularization

• 既存のLRA手法のアプローチ：学習済みのパラメータテンソルを分解する
• 提案手法：学習時、パラメータ同士の共線性が高くなる方へ正則化を行う
  • 正則化項の計算方法
    • 任意のパラメータ2個($ \mathbf{W_i}, \mathbf{W_j} $)を取り出し、$\mathbf{W_i}$ を $\mathbf{W_j}$ へ近づけることを考える
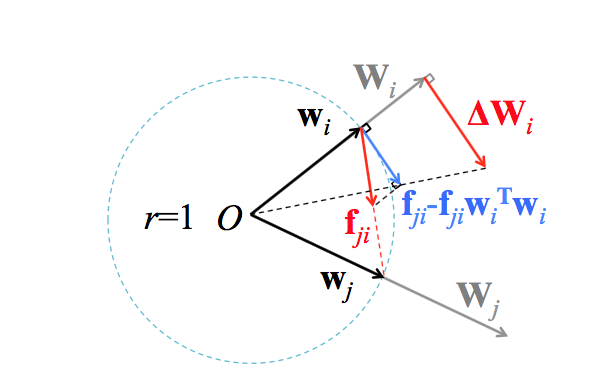
      • パラメータ$ \mathbf{W_i} $を大きさ1に正規化する($ \mathbf{w_i} $)
      • 他のパラメータ$ \mathbf{w_j} $へ近づける方向のベクトル$ \mathbf{f_{ji}} $
        • $ \mathbf{f_{ji}}$ の大きさとしては $ \mathbf{\Delta w_{ji}} = \mathbf{w_j} - \mathbf{w_i}$ のL2, L1ノルムを使用する場合をそれぞれ検討。
      • $ \mathbf{f_{ji}} $による減少分だけ $\mathbf{w_j} $のノルムを増大させる項を追加したもの（図中、青色のベクトル）が正則化項に相当
        • これがないと、全てのパラメータが $\mathbf{0}$ に収束してしまう
      • この正則化項を元の大きさに戻した $ \mathbf{\Delta W_i} $が最終的な正則化項
    • 以上の処理を全てのパラメータペアについて行う事を考えると、これは簡単な行列演算に帰着できるので高速に処理できる

実験

正則化項のノルムのランク

実験設定

• 正則化なし・L1ノルム・L2ノルムの3種類で学習を行う
  • ConvNet + CIFAR-10
  • AlexNet + ImageNet
• 学習済みパラメータをPCAにかけ、累積寄与率95%以上になるまでパラメータを選択した

結果

• 入力に近い層では正則化の効果は殆ど無い
• 層が進むに連れ、正則化の効果が大きく現れる
  • AlexNetのconv3, conv4などでは正則化によってパラメータのランクが1/3に
• 概してL2ノルムのほうが良いパフォーマンスになった

SoTA LRA手法との速度の比較

• test時のパフォーマンスを比較
• 既存手法はスケールしなかった(適用したらむしろ速度が落ちた(?))
• 提案手法ではAlexNetがGPUで2.03xになった。

LRAとSparse DNNの併用

• 低ランク分解したパラメータをスパース化
• 従来のスパース化手法と同等の圧縮率で、勝つ高速化を達成

思ったこと

• test時の速度・精度を比較しているが、train時はどうなのか?
  • 1itertaionあたりの時間、及び収束までのiteration数